gracias por pasar por pasar por mi nuevo blog . para dejarle una enseñanza y aprendizaje de trigonométrica analítica, geometría analítica , estadística
EN ESTE NUEVO BLOG ENCONTRAMOS UNA MANERA DE APRENDER FÁCIL ALGUNOS TEMAS DE TRIGONOMÉTRICA COMO : TRIGONOMÉTRICA ANALÍTICA , GEOMETRÍA ANALÍTICA, ESTADÍSTICA
sábado, 14 de noviembre de 2015
GEOMETRÍA ANALÍTICA
GEOMETRÍA ANALÍTICA
CÓNICAS:
Superficie cónica de revolución
se conoce como superficie de revolución aquella superficie generada por una curva por una curva plana que se hace girara al rededor de una recta fija ubicada en el mismo plano de la curva
se genera cuando una recta llamada GENERATRIZ (G) gira a el rededor del eje de la superficie
sección cónica
se denomina sección cónica (o simplemente cónica ) a la curva intersección de un cono con
un plano que no pasa por su vértice. se clasifican en tres tipos : elipses, parábolas e hiperbolizas .
en el gráfico se muestra las intersección :
* es una curva obtenida por la intersección de un plano con una superficie cónica de la revolución
dependiendo de la forma en que el plano corta la superficie cónica, la curva obtenida
ELIPSE:
Elipse: Se define como el lugar geométrico de los puntos cuya suma de distancias no dirigidas a dos puntos fijo llamado foco es constante.
Ecuaciones canónicas de la elipse con centro en (0,0)
La
elipse es el lugar geométrico de los puntos tales que la suma de sus distancias
a dos puntos fijos llamados focos es constante.
En una elipse se pueden reconocer los
siguientes elementos:
· EJES DE SIMETRIA: Rectas que permiten
reflejar una mitad de la elipse sobre la otra. Una elipse tiene dos ejes:
EJE
MAYOR o eje focal, sobre el cual se
encuentran los focos EV.
EJE
MENOR o eje secundario MM´.
· FOCOS: Puntos fijos F1 y F2 ubicados sobre
el eje mayor.
· CENTRO: Punto medio entre
los focos. Es además el punto donde se interceptan el eje mayor y el eje menor
( C ).
· Vértices: Puntos de la elipse
que se interceptan con los ejes de simetría, se les llama:
Vértices menores, a los ubicados sobre el eje
menor M, M´.
Vértices mayores, a los ubicados sobre el eje mayor E, V.
· SEMIEJES. Segmentos que unen
el centro con uno de los vértices. Se les llama; Semieje mayor, si une el
centro con un vértice mayor es el semieje más largo CV y lo llamamos a.
Semieje menor, une el centro con un
vértice menor es el semieje más corto CM
y lo llamamos b.
NOTA : La distancia del centro a
un vértice mayor , que llamamos
a , es igual a la
distancia del foco a un
vértice menor; c es la
distancia del foco al centro y se puede
obtener por el teorema de Pitagoras
· CUERDA. Es un segmento que
une dos puntos cualesquiera de la elipse
· Cuerda FOCAL. Es una cuerda que pasa
por uno de los focos AB
· DIÁMETRO.
Es una
cuerda que pasa por el centro MM´ ó EV
· LADO
RECTO: es una cuerda focal al eje principal QR. La elipse posee
dos lados rectos
·
Centro: C = ( h , k )
- Distancia entre los vértices: 2.a ó 2.b
- Distancia entre los dos focos 2c.
- Longitud del eje mayor: 2.a ó 2.b
- Longitud del eje menor: 2.a ó 2.b
- Las
coordenadas de los vértices
Si a > b eje principal
paralelo al eje x
V1 = ( h – a , k ) ; V2 =( h + a , k )
- Las coordenadas de los focos si a > b F1
= ( h – c , k ) ; F2
= ( h + c , k )
- Las
coordenadas de los vértices
Si a < b eje principal
paralelo al eje y
V1 = ( h , k – b ) ;
V2 = ( h , k + b )
- Las coordenadas de los focos si a < b F1 = ( h , k – c ) ; F2 = ( h , k + c ) donde c = a-b
- Longitud del lado recto es 2y= 2b
- 2
Ecuación canónica de la elipse con centro en (h,k)
vídeo
Ecuación general de la elipse
Si el centro de la elipse C(x0, y0) y el eje principal es paralelo a OX, los focos tienen de coordenadas F(x0+c, y0) y F'(x0−c, y0). Y la ecuación de la elipse será:

Al quitar denominadores y desarrollar se obtiene, en general, una ecuación de la forma:

Donde A y B tienen el mismo signo.
estadística
métodos numéricos para la caracterización de variables
medidas de localización:
las medidas de localización dividen la distribución en pares iguales, sirven para clasificar a individuos o elementos dentro de una determinada población o muerta
Media: X = Σ xi
n
Mediana: Pares 12345678 → 4+5
2
Impares 1234567 → 4
Moda: Datos que mas se repiten , pueden ser 3 formas
- Modales: números que se repiten una sola vez → 1223456789
- Bimodales: números que se repiten dos veces → 12233456789
- Multimodales: números que se repiten mas de dos veces →1223344556789
- Amodales: Los números no tienes repeticiones → 123456789
Percentiles: Los percentiles son los 99 valores que dividen la serie de datos en 100 partes iguales.
i = P . n
100
Deciles: Deciles son los 9 valores que dividen la serie de datos en 10 partes iguales.
i = P . n
10
Cuartiles: Son los 3 valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales. Q1, Q2, Q3 determinan los valores correspondientes al 25%, 50% y 75% de los datos.
Q1 = 25 . n
100
Medidas de variabilidad
Las medidas de variabilidad nos informan sobre el grado de concentración o dispersión que presentan los datos respecto a su promedio. Llamaremos homogénea, concentrada o poco dispersa a aquella distribución en la que todos los datos están cercanos al centro, como 4 4 5 5 5 5 6 6 6 6 7, y heterogénea o dispersa a la distribución con datos más separados del centro, como 1 3 5 8 10 16 20.
RANGO
También llamado Recorrido o Amplitud total, es la diferencia entre el máximo valor del conjunto de datos y el mínimo de ellos. A mayor rango, mayor dispersión.
El rango del conjunto 4 6 4 7 8 6 5 3 4 7 7 9 6 5 es 6, la diferencia entre el máximo 9 y el mínimo 3.
A veces se usa el Rango verdadero que consiste en considerar cada dato rodeado de una unidad, por efecto de los redondeos, con lo que en el ejemplo anterior el mínimo sería 2,5 y el máximo 9,5. Con ello el rango se convertiría en 7.
No es una medida buena, pues ignora todo lo que ocurre dentro de ese rango.
VARIANZA
Es una medida muy sensible de la variabilidad y base de muchas técnicas estadísticas.
Junto con la media forma el conjunto más importante de medidas.
Es propia de las medidas de intervalo o razón. Su inconveniente es que no usa la misma unidad que los datos, sino su cuadrado.
No se deben comparar varianzas en conjuntos de unidades muy distintas, como estatura e inteligencia.
En teoría del muestreo se sustituye por la cuasi-varianza, de idéntica fórmula, pero con cociente N-1 en lugar de N. En este caso no sería válida la segunda fórmula.
DESVIACIÓN MEDIA
Es una medida de la dispersión consistente en la media aritmética de las desviaciones individuales respecto a la media, tomadas en valor absoluto. También se usan desviaciones respecto a la mediana.
DESVIACIÓN TÍPICA
Es la raíz cuadrada de la anterior. Su objeto es conseguir medir la variabilidad en las mismas unidades que los datos. Así, un conjunto medido en metros, tendrá la varianza medida en metros cuadrados, pero la desviación típica en metros.
Como en la varianza, para datos aislados basta con suprimir las frecuencias ni.
La desviación típica s es base de muchas técnicas, al igual que la media y la varianza. Su gran ventaja es estar medida en las mismas unidades que los datos y la media, lo que permite establecer razones y proporciones entre ellas.
La desviación típica cumple la llamada desigualdad de Tchebychev: según la cual, los datos que se alejan de la media una distancia igual o menor que s, multiplicado por un coeficiente k suponen más de la proporción 1-1/k2. Así, el 75% de los datos al menos, se encuentra a menos de dos desviaciones típicas y el 89% a menos de tres.
la desviación estándar:
es una medida de la variación de los valores con respecto a la medida. Es una especie de desviación promedio con respecto a la media. su formula es:
S= √∑(x-X)2/n
Donde:
X= media
x=valores de los datos
n= numero de datos
∑= sumatoria
Nota:
° El valor de la desviacion estandar "s" es positivo. Resulta ser cero cuando todos los valores de los datos son el mismo número.
°El valor de la desviación estándar se puede incrementar de manera importante cuando se incluye uno o más datos distantes, es decir, datos que se encuentran muy lejos de los demás.
° las unidades "s" son las mismas de los datos originales.
PROCEDIMIENTO PARA CALCULAR LA DESVIACIÓN ESTÁNDAR:
1) Calcular el valor de la Media
2) Restar la media de cada valor individual para tener una lista de desviaciones de la forma (x-X)
3) elevar al cuadrado cada de las diferencias obtenidas en el paso anterior. Recuerda que al elevar al cuadrado un número negativo éste se vuelve positivo. (x-X)2
4) Sumar todos los resultados obtenidos en el paso anterior el cual es: ∑(x-X)2
5)Dividir el total del paso 4 entre el número de datos n
6) Calcular la raíz cuadrada del resultado anterior
trigonometria analitica
IDENTIDADES TRIGONOMÉTRICAS
DEFINICIÓN :
Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones.Las identidades trigonométricas nos permiten plantear una misma expresión de diferentes formas. Para simplificar expresiones algebraicas, usamos la factorización, denominadores comunes, etc. Pero para simplificar expresiones trigonométricas utilizaremos estas técnicas en conjunto con las identidades trigonométricas.
Antes de comenzar a ver las diferentes identidades trigonométricas, debemos conocer algunos términos que usaremos bastante en trigonometría, que son las tres funciones más importantes dentro de esta. El coseno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto adyacente y la hipotenusa:
Otra función que utilizaremos en trigonometría es “seno”. Definiremos seno como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo:
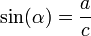
Mientras tanto la palabra tangente en matemática puede que tenga dos significados distintos. En geometría se utiliza el término de recta tangente, pero a nosotros en trigonometría nos interesa otro término que es el de tangente de un ángulo, el cual es la relación entre los catetos de un triángulo rectángulo , lo mimo que decir que es el valor numérico que resulta de dividir la longitud del cateto opuesto entre la del cateto adyacente al ángulo.
Otra función que utilizaremos en trigonometría es “seno”. Definiremos seno como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo:
Mientras tanto la palabra tangente en matemática puede que tenga dos significados distintos. En geometría se utiliza el término de recta tangente, pero a nosotros en trigonometría nos interesa otro término que es el de tangente de un ángulo, el cual es la relación entre los catetos de un triángulo rectángulo , lo mimo que decir que es el valor numérico que resulta de dividir la longitud del cateto opuesto entre la del cateto adyacente al ángulo.

Es llamada identidad trigonométrica fundamental, y efectuando sencillas operaciones permite encontrar unas 24 identidades más, muy útiles para problemas introductorios del tipo conocido el valor de la función seno, obtenga el valor de las restantes (sin tabla ni calculadora).
Por ejemplo, si se divide ambos miembros de "sen² + cos² = 1" por cos², se obtiene:
Ahora, dividiendo ambos miembros de la misma expresión por el sen², se obtiene:
Entonces puede expresarse la función seno según alguna otra conocida:

que es identidad:
una identidad es una igualdad entre dos expresiones que contiene una o mas variable, y que es valida para todo valor de la variable en que las expresiones estén definidas .
Pueden demostrarse según la Fórmula de Euler o mediante la proyección de ángulos consecutivos. La identidad de la tangente surge del cociente entre coseno y seno, y las restantes de la recíproca correspondiente.
Identidades para ángulos dobles
Pueden obtenerse emplazándolo y por x (o sea  ) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando
) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando  .
.
 ) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando
) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando  .
.






Transformación de productos en suma diferencias

ver vídeo

ver vídeo
ECUACIONES TRIGONOMÉTRICAS
En las ecuaciones trigonométricas la incógnita es el ángulo común de las funciones trigonométricas. No puede especificarse un método general que permita resolver cualquier ecuación trigonométrica; sin embargo, un procedimiento efectivo para solucionar un gran número de éstas consiste en transformar, usando principalmente las identidades trigonométricas, todas las funciones que aparecen allí en una sola función (es recomendable pasarlas todas a senos o cosenos). Una vez expresada la ecuación en términos de una sola función trigonométrica, se aplican los pasos usuales en la solución de ecuaciones algebraicas para despejar la función; por último, se resuelve la parte trigonométrica, es decir, conociendo el valor de la función trigonométrica de un ángulo hay que pasar a determinar cuál es ese ángulo.
Ecuaciones trigonométricas lineales
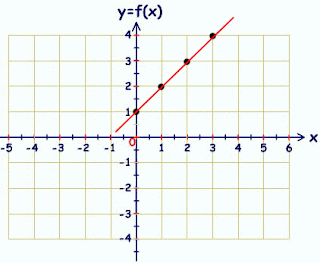
es una función polifónica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
Las funciones se pueden clasificar en tres tipos:
- Si el valor de “m” es mayor a cero la función es creciente.
- Si el valor de “m” es menor a cero la función es decreciente.
- Si “m” es igual a cero la función es constante (su gráfica será una recta paralela al eje X).
es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
Las funciones se pueden clasificar en tres tipos:
- Si el valor de “m” es mayor a cero la función es creciente.
- Si el valor de “m” es menor a cero la función es decreciente.
- Si “m” es igual a cero la función es constante (su gráfica será una recta paralela al eje X).
Escriba la ecuación original, como sin ^ 2 (x) + sin (x) = 1. Luego, escribe un dejar que la declaración que sustituirá una variable para la función trigonométrica. Por ejemplo, vamos a = sin (x). Vuelva a escribir la ecuación original y sustituya la letra que eligió en su sentencia let para la función trigonométrica. Sin ^ 2 (x) + sin (x) = 1 se convertirían en 2a ^ 2 + a = 1
Establezca la ecuación es igual a cero mediante el uso de álgebra para poner todas las variables y constantes de la izquierda y ordenar los exponentes en orden descendente. Por ejemplo, tendría que restar 1 a ambos lados de 2a ^ 2 + a = 1 para obtener 2a ^ 2 + a – 1 = 0.
Multiplique el coeficiente principal por la constante en el extremo. En este caso, lo haría múltiple con 2 -1 -2 conseguir. A continuación, averiguar qué dos números multiplicados juntos haría que esa respuesta y se suman al coeficiente en el medio. Por ejemplo, podría determinar que el 2 y -1 se multiplican para hacer -2 y sumar a 1 que es el coeficiente medio en 2a ^ 2 + a – 1.
Utilice los dos números que encontraste para dividir el término medio (trozo) de su ecuación en dos nuevos términos con esos números como coeficientes. Por ejemplo, usted pondría 2 y -1 en los espacios en blanco de la 2a ^ 2 + a + ___ ___ un -1 para obtener 2a ^ 2 + 2a – a – 1.
Grupo de los cuatro términos en parejas de dos. Entonces, el factor de la mayor común divisor (MCD) que pueda sacar de la primera serie. Se podría factorizar 2a de ambos 2a ^ 2 y 2 bis, para conseguir lo siguiente: 2a (a 1).
nuevo en un segundo conjunto de paréntesis como éste: 2a (a + 1) ___ (a 1). Mira este formulario y la forma de la ecuación antes de que éste pueda verificar lo que tendría que multiplicar cada término del segundo paréntesis con volver a la original. Escribe este número y su signo, positivo o negativo, el espacio en blanco. Aquí usted llegar a 2a (a 1) -. 1 (a 1) = 0 Combina las dos piezas fuera de cada conjunto de paréntesis en un factor y luego escribir una copia de lo que hay en los dos conjuntos de paréntesis, como la otro factor. En este caso, se debe terminar con (2a – 1) (a 1) = 0.
Establezca cada factor igual a cero y resubstitute la función trigonométrica para la letra de acuerdo a su declaración let. Por ejemplo, (2a – 1) (un 1) = 0 se convertirían en 2sin (x) – 1 = 0 y senx 1 = 0 Entonces, aislar la función trigonométrica en cada ecuación usando la manipulación algebraica.. Por ejemplo, 2sin (x) – 1 = 0 se convertiría en el pecado (x) = 1/2
Utilice un círculo de unidades, calculadora o ángulos trigonometría memorizados para tomar la inversa de la función trigonométrica y aislar el ángulo para el cual usted está resolviendo. Por ejemplo, el seno inverso de media sería de 30 grados y 150 grados. Enumere todas las soluciones posibles de ambos factores como sus respuestas.
ver este vídeo
Ecuaciones trigonométricas con identidades
vídeo
Ecuaciones trigonométricas con identidades para ángulos dobles y medios
ángulos dobles
Las identidades de ángulo doble (estas realmente son solo casos especiales de las fórmulas de Bhaskara Acharya, donde u = v )


Ejemplo:
Reescriba en una forma más simple usando una identidad trigonométrica:
2sin(5p)cos(5p)
Usando la fórmula de ángulo doble para el seno, donde

Aplicando la fórmula, obtenemos
ángulos medios

Ejemplo:
Determine el valor correcto de cos15° .

• Recordar que para
una función, f, tenga
inversa , f
-1
, es
necesario que f sea
una función uno-a-uno.
o Una función, f, es
uno-a-uno si para
cada a ≠ b en el
dominio de f, f(a) ≠
f(b).
o (Cualesquiera dos x
diferentes producen
dos y’s diferentes.)
La función
inversa, f
-1
,
invierte la
correspondencia
dada por f .
• Esto es, si el par
ordenado (u,v)
pertence a f,
entonces (v, u)
pertenece f
Suscribirse a:
Entradas (Atom)