IDENTIDADES TRIGONOMÉTRICAS
DEFINICIÓN :
Estas identidades son siempre útiles para cuando necesitamos simplificar expresiones que tienen incluidas funciones trigonométricas, cualesquiera que sean los valores que se asignen a los ángulos para los cuales están definidas estas razones.Las identidades trigonométricas nos permiten plantear una misma expresión de diferentes formas. Para simplificar expresiones algebraicas, usamos la factorización, denominadores comunes, etc. Pero para simplificar expresiones trigonométricas utilizaremos estas técnicas en conjunto con las identidades trigonométricas.
Antes de comenzar a ver las diferentes identidades trigonométricas, debemos conocer algunos términos que usaremos bastante en trigonometría, que son las tres funciones más importantes dentro de esta. El coseno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto adyacente y la hipotenusa:
Otra función que utilizaremos en trigonometría es “seno”. Definiremos seno como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo:
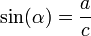
Mientras tanto la palabra tangente en matemática puede que tenga dos significados distintos. En geometría se utiliza el término de recta tangente, pero a nosotros en trigonometría nos interesa otro término que es el de tangente de un ángulo, el cual es la relación entre los catetos de un triángulo rectángulo , lo mimo que decir que es el valor numérico que resulta de dividir la longitud del cateto opuesto entre la del cateto adyacente al ángulo.
Otra función que utilizaremos en trigonometría es “seno”. Definiremos seno como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo:
Mientras tanto la palabra tangente en matemática puede que tenga dos significados distintos. En geometría se utiliza el término de recta tangente, pero a nosotros en trigonometría nos interesa otro término que es el de tangente de un ángulo, el cual es la relación entre los catetos de un triángulo rectángulo , lo mimo que decir que es el valor numérico que resulta de dividir la longitud del cateto opuesto entre la del cateto adyacente al ángulo.

Es llamada identidad trigonométrica fundamental, y efectuando sencillas operaciones permite encontrar unas 24 identidades más, muy útiles para problemas introductorios del tipo conocido el valor de la función seno, obtenga el valor de las restantes (sin tabla ni calculadora).
Por ejemplo, si se divide ambos miembros de "sen² + cos² = 1" por cos², se obtiene:
Ahora, dividiendo ambos miembros de la misma expresión por el sen², se obtiene:
Entonces puede expresarse la función seno según alguna otra conocida:

que es identidad:
una identidad es una igualdad entre dos expresiones que contiene una o mas variable, y que es valida para todo valor de la variable en que las expresiones estén definidas .
Pueden demostrarse según la Fórmula de Euler o mediante la proyección de ángulos consecutivos. La identidad de la tangente surge del cociente entre coseno y seno, y las restantes de la recíproca correspondiente.
Identidades para ángulos dobles
Pueden obtenerse emplazándolo y por x (o sea  ) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando
) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando  .
.
 ) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando
) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando  .
.




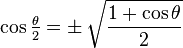


Transformación de productos en suma diferencias

ver vídeo

ver vídeo
ECUACIONES TRIGONOMÉTRICAS
En las ecuaciones trigonométricas la incógnita es el ángulo común de las funciones trigonométricas. No puede especificarse un método general que permita resolver cualquier ecuación trigonométrica; sin embargo, un procedimiento efectivo para solucionar un gran número de éstas consiste en transformar, usando principalmente las identidades trigonométricas, todas las funciones que aparecen allí en una sola función (es recomendable pasarlas todas a senos o cosenos). Una vez expresada la ecuación en términos de una sola función trigonométrica, se aplican los pasos usuales en la solución de ecuaciones algebraicas para despejar la función; por último, se resuelve la parte trigonométrica, es decir, conociendo el valor de la función trigonométrica de un ángulo hay que pasar a determinar cuál es ese ángulo.
Ecuaciones trigonométricas lineales
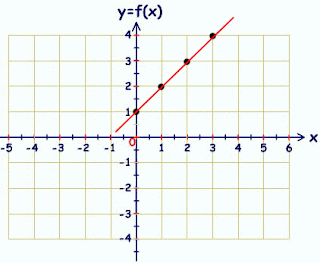
es una función polifónica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
Las funciones se pueden clasificar en tres tipos:
- Si el valor de “m” es mayor a cero la función es creciente.
- Si el valor de “m” es menor a cero la función es decreciente.
- Si “m” es igual a cero la función es constante (su gráfica será una recta paralela al eje X).
es una función polinómica de primer grado, en un gráfica se representa como una línea recta y se escribe: f(x) = mx + b.
Recordemos que los polinomios de primer grado tienen la variable elevada a la primera potencia, cuando la potencia es 1 normalmente no se escribe.
m = pendiente de la recta (constante).
b = punto de corte de la recta con el eje y (constante).
x = variable.
Cuando modificamos “m” en una función lineal se modifica la pendiente es decir la inclinación de la recta, si cambiamos “b” la línea se mueve hacía arriba o abajo.
Las funciones se pueden clasificar en tres tipos:
- Si el valor de “m” es mayor a cero la función es creciente.
- Si el valor de “m” es menor a cero la función es decreciente.
- Si “m” es igual a cero la función es constante (su gráfica será una recta paralela al eje X).
Escriba la ecuación original, como sin ^ 2 (x) + sin (x) = 1. Luego, escribe un dejar que la declaración que sustituirá una variable para la función trigonométrica. Por ejemplo, vamos a = sin (x). Vuelva a escribir la ecuación original y sustituya la letra que eligió en su sentencia let para la función trigonométrica. Sin ^ 2 (x) + sin (x) = 1 se convertirían en 2a ^ 2 + a = 1
Establezca la ecuación es igual a cero mediante el uso de álgebra para poner todas las variables y constantes de la izquierda y ordenar los exponentes en orden descendente. Por ejemplo, tendría que restar 1 a ambos lados de 2a ^ 2 + a = 1 para obtener 2a ^ 2 + a – 1 = 0.
Multiplique el coeficiente principal por la constante en el extremo. En este caso, lo haría múltiple con 2 -1 -2 conseguir. A continuación, averiguar qué dos números multiplicados juntos haría que esa respuesta y se suman al coeficiente en el medio. Por ejemplo, podría determinar que el 2 y -1 se multiplican para hacer -2 y sumar a 1 que es el coeficiente medio en 2a ^ 2 + a – 1.
Utilice los dos números que encontraste para dividir el término medio (trozo) de su ecuación en dos nuevos términos con esos números como coeficientes. Por ejemplo, usted pondría 2 y -1 en los espacios en blanco de la 2a ^ 2 + a + ___ ___ un -1 para obtener 2a ^ 2 + 2a – a – 1.
Grupo de los cuatro términos en parejas de dos. Entonces, el factor de la mayor común divisor (MCD) que pueda sacar de la primera serie. Se podría factorizar 2a de ambos 2a ^ 2 y 2 bis, para conseguir lo siguiente: 2a (a 1).
nuevo en un segundo conjunto de paréntesis como éste: 2a (a + 1) ___ (a 1). Mira este formulario y la forma de la ecuación antes de que éste pueda verificar lo que tendría que multiplicar cada término del segundo paréntesis con volver a la original. Escribe este número y su signo, positivo o negativo, el espacio en blanco. Aquí usted llegar a 2a (a 1) -. 1 (a 1) = 0 Combina las dos piezas fuera de cada conjunto de paréntesis en un factor y luego escribir una copia de lo que hay en los dos conjuntos de paréntesis, como la otro factor. En este caso, se debe terminar con (2a – 1) (a 1) = 0.
Establezca cada factor igual a cero y resubstitute la función trigonométrica para la letra de acuerdo a su declaración let. Por ejemplo, (2a – 1) (un 1) = 0 se convertirían en 2sin (x) – 1 = 0 y senx 1 = 0 Entonces, aislar la función trigonométrica en cada ecuación usando la manipulación algebraica.. Por ejemplo, 2sin (x) – 1 = 0 se convertiría en el pecado (x) = 1/2
Utilice un círculo de unidades, calculadora o ángulos trigonometría memorizados para tomar la inversa de la función trigonométrica y aislar el ángulo para el cual usted está resolviendo. Por ejemplo, el seno inverso de media sería de 30 grados y 150 grados. Enumere todas las soluciones posibles de ambos factores como sus respuestas.
ver este vídeo
Ecuaciones trigonométricas con identidades
vídeo
Ecuaciones trigonométricas con identidades para ángulos dobles y medios
ángulos dobles
Las identidades de ángulo doble (estas realmente son solo casos especiales de las fórmulas de Bhaskara Acharya, donde u = v )


Ejemplo:
Reescriba en una forma más simple usando una identidad trigonométrica:
2sin(5p)cos(5p)
Usando la fórmula de ángulo doble para el seno, donde

Aplicando la fórmula, obtenemos
ángulos medios

Ejemplo:
Determine el valor correcto de cos15° .

• Recordar que para
una función, f, tenga
inversa , f
-1
, es
necesario que f sea
una función uno-a-uno.
o Una función, f, es
uno-a-uno si para
cada a ≠ b en el
dominio de f, f(a) ≠
f(b).
o (Cualesquiera dos x
diferentes producen
dos y’s diferentes.)
La función
inversa, f
-1
,
invierte la
correspondencia
dada por f .
• Esto es, si el par
ordenado (u,v)
pertence a f,
entonces (v, u)
pertenece f


















No hay comentarios:
Publicar un comentario